Python套件 - RSA的計算 - pycryptodome

RSA – 公鑰加密，私鑰解密。

本篇將帶領您實際實作RSA的CTF練習題。

RSA是什麼?

RSA是一個非對稱加密演算法，利用兩個質數作為加密與解密的兩個金鑰(Key)，在1978年美國麻省理工學院的 Ron Rivest, Adi Shamir, Leonard Adleman 三位發明者的名字去發展並命名，目前是最流行的公開金鑰演算法之一，可作為資料加密及數位簽署的功能。

RSA的安全取決於質因數分解的困難度，其公鑰和私鑰是一對大質數的函數。從一個公鑰和密文恢復出明文的難度，等價於分解兩個大質數之積。

質數是指在一個大於1的自然數中，除了1和此整數自身外，不能被其他自然數整除的數。

互質數是指如果兩個或兩個以上的整數的最大公因數是 1，則稱它們為互質。

其餘數學觀念與名詞可參考羊小咩撰寫的 Day 23. 非對稱式加密演算法 – RSA (觀念篇) 。

RSA 演算法

選兩個大質數 p 和 q (至少100位數)，令 N = p • q
再計算Ø(N)=(p-1)(q-1)，並選一個與Ø(N)互質數 e
(e,N) 即為公開金鑰加密法為 C = M^e mod N
選一個數 d，滿足 e • d mod Ø(N) = 1
d 即為解密金鑰(亦稱私有金鑰或祕密金鑰)
解密法為 M = C^d mod N

Ø(N)為Euler’s Totient函數，其意為與N互質之個數。

加密

M 的 e 次方除以 N 求餘數 C

解密

C 的 d 次方除以 N 求餘數 M

例子

接收方選 p=3 ， q=11 ; 此時 N = p • q = 33
找出 1 個與 ( p-1 ) x ( q-1 ) = ( 3-1 )( 11-1 ) = 2 x 10 = 20
互質數 e=3
( e, N) = (3,33) 即為接收方的公開金鑰
接收方選一個數 d=7 當作解密金鑰，
滿足 e • d ≡ 1 mod 20 ( 7 x 3 ≡ 1 mod 20 )
令明文 M = 19
加密 : C = Me mod N = 193 mod 33 = 28
解密 : M = Cd mod N = 287 mod 33 = 19

操作演練

Mind your Ps and Qs

Category: Cryptography
AUTHOR: SARA

In RSA, a small e value can be problematic, but what about N? Can you decrypt this?

Decrypt my super sick RSA:
c: c = 62324783949134119159408816513334912534343517300880137691662780895409992760262021
n = 1280678415822214057864524798453297819181910621573945477544758171055968245116423923
e: 65537

解法

根據題目要求，我們知道
c是密文、n是p*q的結果。 e = (p-1)*(q-1)
寫成虛擬碼，我們要做的就是找到p跟q的值。

C = ciphertext
p and q = prime numbers
n = p * q
phi = (p-1) * (q-1)
e = some number that 1 < e < phi and gcd(e,phi) == 1 
d = e^(-1) mod phi

質因數分解直接算會到天荒地老，直接去查Factordb比較快。

它還有python套件呢! https://github.com/ryosan-470/factordb-python

貼上後的結果。

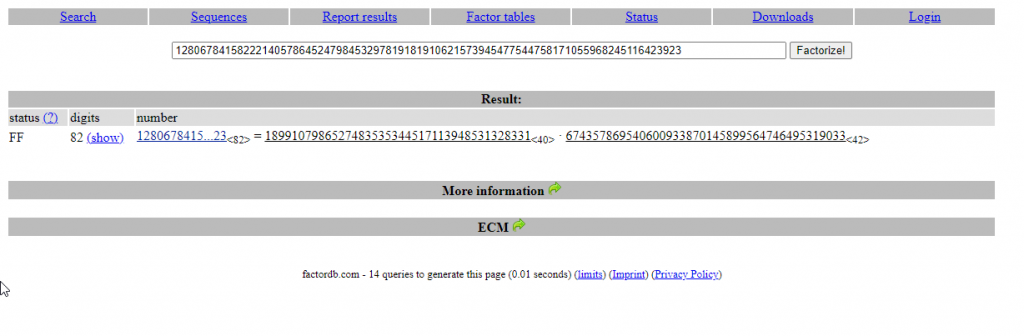
我們得知
p = 1899107986527483535344517113948531328331
q = 674357869540600933870145899564746495319033

接下來可以開始計算明文是什麼了，接下來才是我們的主角 – python cryptodome上場了。

PyCryptodome其實就是PyCrypto的擴充。

https://pypi.org/project/pycrypto/

但最後Released是2013年，所以還是用PyCryptodome來做吧，最後更新是2021，而且支援Python 2.7、3.5、PyPy。

https://pypi.org/project/pycryptodome/

安裝方式

pip install pycryptodome

撰寫還原明文python code

from Crypto.Util.number import inverse, long_to_bytes

c = 843044897663847841476319711639772861390329326681532977209935413827620909782846667
c = 62324783949134119159408816513334912534343517300880137691662780895409992760262021
n = 1280678415822214057864524798453297819181910621573945477544758171055968245116423923
e = 65537
p = 1899107986527483535344517113948531328331
q = 674357869540600933870145899564746495319033

phi = (p-1)*(q-1)

d = inverse(e, phi)

m = pow(c,d,n)

print(long_to_bytes(m))

實際執行

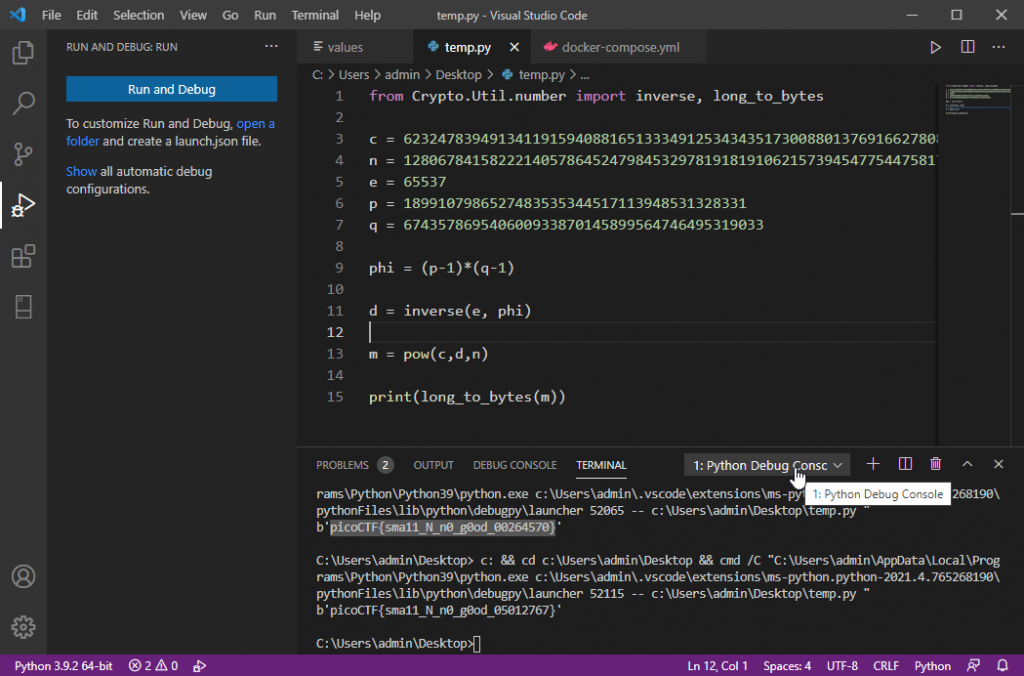
將產生的flag拿去驗證。

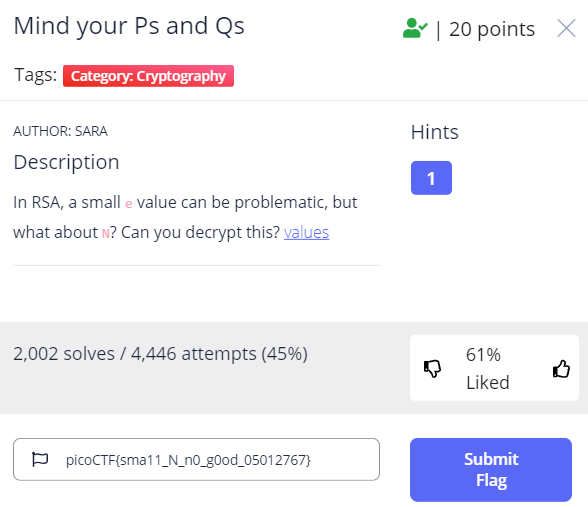
成功! 喜歡我的文章請給我免費拍拍手~

參考資料：

RSA公開金鑰密碼機制 http://mslab.csie.asia.edu.tw/~jackjow/courses/992_InfoSecurity/ppts/IS_RSA.pdf
維基百科 – RSA加密演算法 https://zh.wikipedia.org/wiki/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95

Python套件 – RSA的計算 – pycryptodome